在 WSL2 Ubuntu20.4 系统中安装 Baltamatica 显示成功, 准备运行时出现 Inconsistency detected by ld.so: dl-call-libc-early-init.c: 37: _dl_call_libc_early_init: Assertion `sym != NULL' failed! 错误.

请问这该怎么处理?谢谢!
写了一个自适应 Simpson 求积公式的代码, 运行过程中出现了 abs命令或者变量的类型发生变化导致,无法求值 的错误, 如图所示

我写的 adapsimp 的代码如下
function [s, err] = adapsimp(func, a, b, tol) s = comsimp(func, a, b, 2); c = (a + b) / 2; s1 = comsimp(func, a, c, 2); s2 = comsimp(func, c, b, 2); s12 = s1 + s2; err = abs(s12 - s) / 15; if err < tol s = s12; else [s1, err1] = adapsimp(func, a, c, tol/2); [s2, err2] = adapsimp(func, c, b, tol/2); s = s1 + s2; err = err1 + err2; end end
里面用到了 comsimp 函数, 是这样写的
function s = comsimp(func, a, b, n)
h = (b - a) / n;
s0 = func(a) + func(b);
s1 = 0; % summation of f(x_{2k-1})
s2 = 0; % summation of f(x_{2k})
for k = 1:n-1
x = a + k * h;
if rem(k , 2) == 0
s2 = s2 + func(x);
else
s1 = s1 + func(x);
end
end
s = h * (s0 + 4 * s1 + 2 * s2) / 3;
end这部分代码在 octave 上运行是没有问题的

用的版本是2.2.0最新版的.
使用 disp 函数给输出增加说明的时候, 出现了顺序上的错误. 比如使用下面一段代码
for n = 1:3
disp("n 的值为")
n
end正常输出应该是一句 "n 的值为" 和 n 的具体值交替输出

但现在是先将n的值都输出完了, 才输出的disp语句里面的内容

使用的是 Deepin 操作系统, 版本为 2.1.1. 好像 Deepin 的安装包还停留在 1 月份的没更新.
对于数量级极大的一组数据
x = 0:0.1:1; y = [2, -2, -6, -42, -1806, -3.26344e+06, -1.06501e+13, -1.13424e+26, -1.28649e+52, -1.65507e+104, -2.73925e+208];
只要使用 plot(x, y) 绘制图形, 软件便会自动退出. 对于其他正常的数据, 绘图时正常的.
使用的是 Deepin 操作系统, 版本为 2.1.1.
目前 Windows 平台下 3.0.1 版的软件是不可以在终端下使用而只能启动图形界面了吗?
使用 mesh 函数绘制曲面图形,报错提示错误使用 mesh 函数,Z 必须为矩阵,不能是标量或向量。
Deepin 系统版本为 2.1.1 上运行是没有问题的,但在 Windows 11 系统版本为 3.0.3 上运行会出现上述错误。
clear;
clc;
% 空间步长
h = 0.01;
% 时间步长
tau = 0.01;
x = 0:h:1;
t = 0:tau:1;
% 剖分网络
[X, T] = meshgrid(x, t);
% 解析解
Ut = exp(-X+T);
% 作图
mesh(x, t, Ut)
title("扩散方程初边值问题的精确解")
xlabel("x")
ylabel("t")另外,Deepin 的版本什么时候更新,半年前反馈的 Deepin 版本上的问题到现在还没有修正。
操作系统为 Deepin20.9, 版本为开发者预览版 Baltamatica_999-3.1.3-dev1.
在终端下启动北太天元并使用绘图函数会自动退出程序,提示需要先创建一个 QApplication 应用。

使用 symbolic 插件提供的 sym 命令创建符号变量 x 后,工作区不显示任何变量信息

使用 whos 命令查看发现只有 ans 这个变量,且类型识别为 extern. 将这个 ans 赋值给 x 之后,无论参与运算工作区都是不显示任何信息的,也就是工作区无法识别 extern 这种类型的变量。
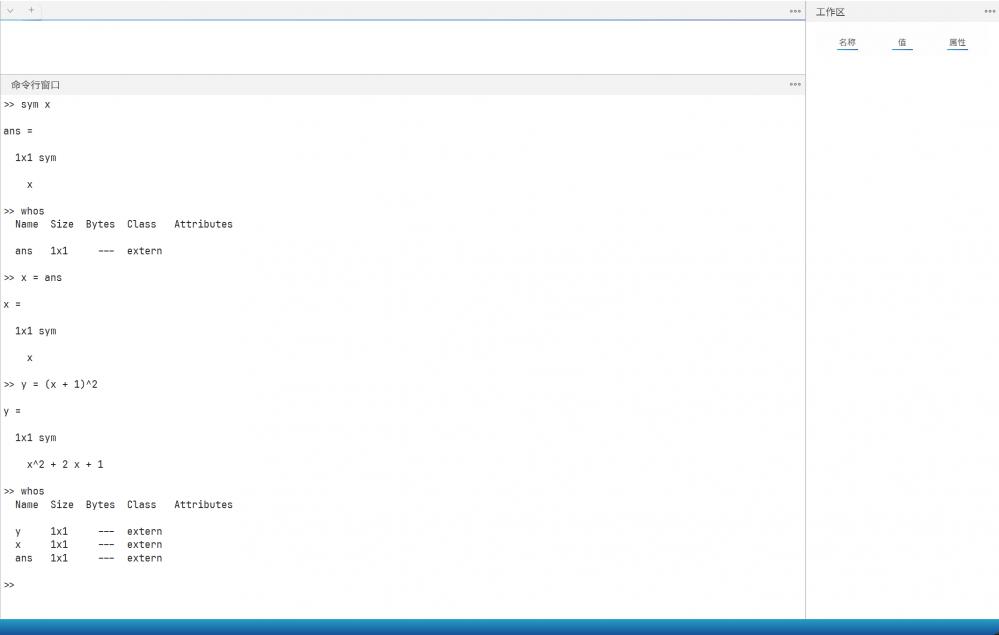
目前将所有公布过的正式版本都安装尝试了一遍,都是这种情况。
操作系统为 Deepin20.9, 安装的版本为 baltamatica_999_3.5.0_dev0
绘制一个周期的正弦曲线, 得到的图如下, 坐标轴上标记的点已经超出了图像的大小.
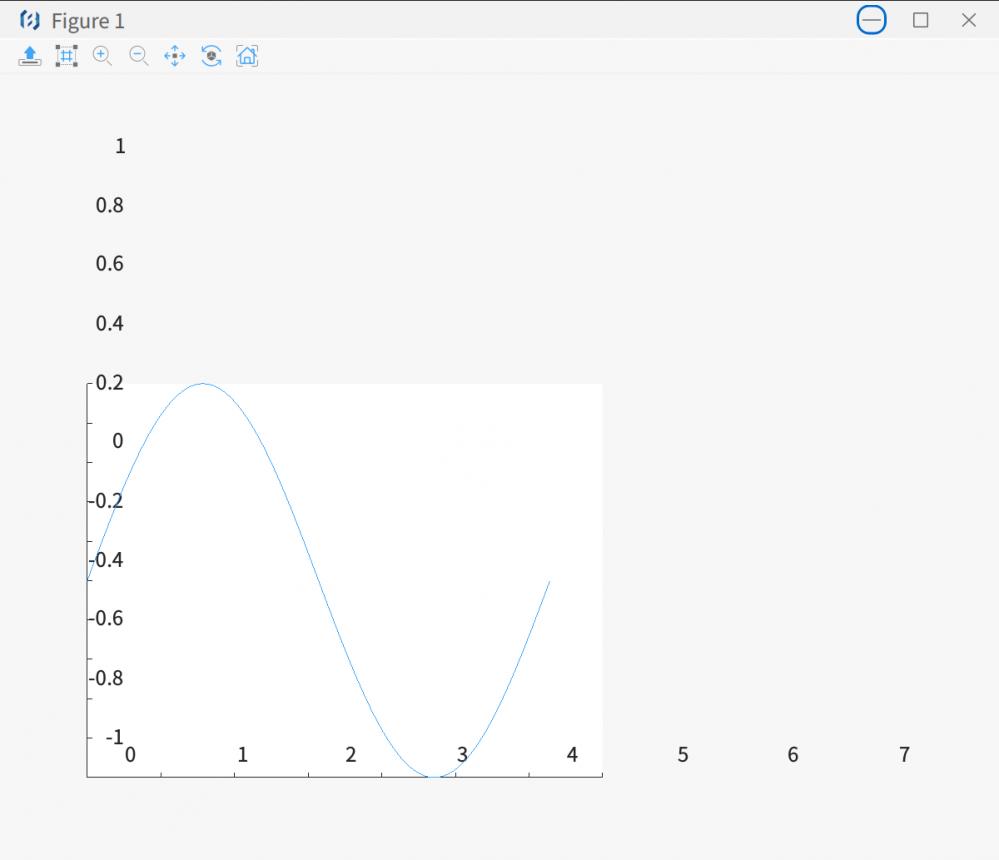
操作系统是 Deepin V23, 输入法使用的是 fcitx5. 从 3.5.0-dev1 开始试验, 到最新的 3.6.1-dev1, 使用通用版的 Linux 安装包安装后, 均无法在编辑器中切换中文输入法输入中文.
3.1.3-dev1_Deepin20.9 在 Deepin V23 上安装能够正常切换中英文.
IQA 插件默认使用的是 qwen2.5 模型,每次重新启动软件都需要重新使用 AIInit 初始化一下其他本地模型。建议增加修改默认模型的功能。
首先生成一个测试文件,第一行类似于表头,2到4行每行存储3个数,用tab键分隔
fwid = fopen("test.txt", "w");
fprintf(fwid, "%s\t%s\t%s\n", "column_1", "column_1", "column_3");
fprintf(fwid, "%d\t%d\t%d\n", 1, 2, 3);
fprintf(fwid, "%d\t%d\t%d\n", 4, 5, 6);
fprintf(fwid, "%d\t%d\t%d\n", 7, 8, 9);
fclose(fwid);得到的文件共5行,第5行是一空行。下面以 fgetl 函数逐行读取该文件。
方法一:
以 feof 函数作为 while 循环的判断条件,依次读取文件的每一行并显示出来
frid = fopen("test.txt", "r");
fgetl(frid);
% 是否到达文件末尾 (EOF)
while ~feof(frid)
line = fgetl(frid);
disp(line);
end
fclose(frid);该方法在北太天元中除了显示文件中的3行数字,还会显示一个-1,这个-1是fgetl判断到文件末尾后返回的。而在 MATLAB 中只显示 3 行数字。


方法二:
考虑到方法一中 fgetl 函数返回了 -1 但 feof 条件没有起作用,将 while 循环条件改为 true,循环内部满足 feof 条件 break 循环。
frid = fopen("test.txt", "r");
fgetl(frid);
while true
line = fgetl(frid);
% 如果到达文件末尾,则退出循环
if feof(frid)
break;
end
disp(line);
end
fclose(frid);该方法在北太天元中输出符合预期,但在 MATLAB 中只输出两行数据


也就是说,在北太天元中,读取了 7 8 9 三个数后,需要再读取一行才到末尾 (EOF),所以读取到的 -1 没有 disp;而在 MATLAB 中,读取了之后已经到末尾,虽然读取了这三个数,就跳出循环不再显示。代码中的 if 判断更换任意位置在北太天元中都将显示 -1。
验证:
手动逐行读取文件进行验证
frid = fopen("test.txt", "r");
fgetl(frid);
disp(feof(frid));
fgetl(frid);
disp(feof(frid));
fgetl(frid);
disp(feof(frid));
fgetl(frid);
disp(feof(frid));
fgetl(frid);
disp(feof(frid));
fclose(frid);在北太天元和 MATLAB 中输出的结果分别是
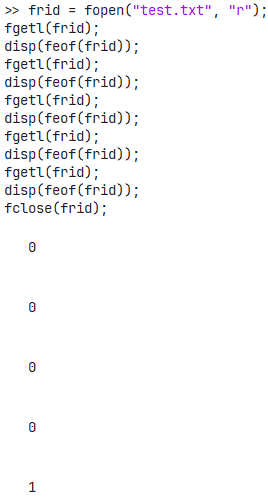
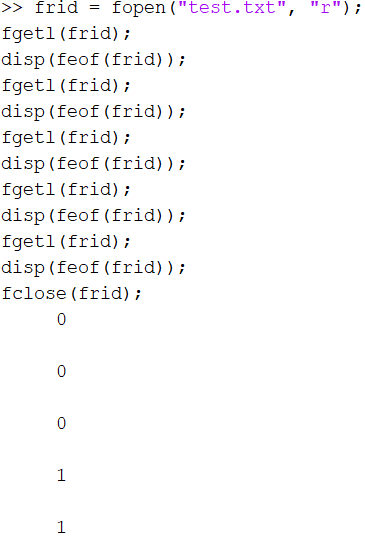
测试文件共 5 行,前四行有内容,第五行是空行,在 MATLAB 中,读取完第四行就判断为文件末尾,而在北太天元中,五行全部读完才判断是文件末尾。
无法读取保存polyshape数据类型的mat数据文件
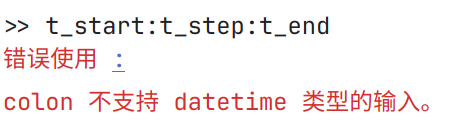
t_start = datetime(2025, 5, 21, 21, 00, 00); t_end = t_start + hours(1); t_step = minutes(1); t_start:t_step:t_end
运行报错, 提示不支持冒号运算符
1. 首先,针对北太天元所使用的 Python,安装 pyttsx3 文本转语音引擎:
load_plugin("Python");
pipcmd("install pyttsx3 -i https://pypi.tuna.tsinghua.edu.cn/simple/");2. 使用如下函数初始化一个基于 pyttsx3 的 TTS 引擎并设置其参数:
function [engine] = textToSpeech_pytts_init()
% 获取 Python 根对象用于调用 Python 函数等
py = pyroot;
% 导入 pyttsx3 模块
pyttsx3 = py.pyttsx3;
% 初始化 TTS 引擎
engine = pyttsx3.init();
% 设置语音属性 (可选)
voices = engine.getProperty('voices');
% voices 是一个 py.list 对象
% 目前北太天元无法直接使用 length 获取 py.list 的长度
% 只能暂时使用 Python 中的 len 来代替
for i = 1:py.len(voices)
% 同样, 北太天元中的 frompy 函数无法将 py.list 类型的 voices 转化为内置的数组
% 所以只能通过 pygetitem 函数来获取每一个元素
voice = pygetitem(voices, i-1);
if contains(string(voice.name), 'Chinese') % 查找支持中文的语音
engine.setProperty('voice', voice.id);
break
end
if contains(string(voice.name), 'English') % 查找支持英文的语音
engine.setProperty('voice', voice.id);
break;
end
end
% 设置语速 (可选)
engine.setProperty('rate', 150); % 默认值为 200
% 设置音量 (可选)
engine.setProperty('volume', 0.8); % 范围是 0.0 到 1.0
end3. 初始化引擎,并传给引擎文本,让引擎朗读,或者保存音频:
% 初始化 TTS 引擎 engine = textToSpeech_pytts_init(); % 设置要说的文本 text = "你好,我在北太天元中调用 Python 文本转语音引擎!"; engine.say(text); % 保存为 WAV 文件 engine.save_to_file(text, "output.wav"); % 运行并等待语音完成 engine.runAndWait(); engine.stop()
这样便可以听见引擎朗读的声音,也可以在本地找到保存的 output.wav 文件。
本示例中的 textToSpeech_pytts_init() 函数参考 大预言模型(LLM)赋能具身智能中的人机交互 中 Python 模型集成一节,并将无法在北太天元中运行的部分进行了修改。
本示例也参考了 Python使用总结之Python文本转语音引擎:pyttsx3完全指南 如何使用 pyttsx3 库。
对于这样一组数据, 每一列数据长度保持一致, 不足的采用空格补充; 数据与数据之间采用空格分隔:
13.52220 0.00 18.100 0 0.6310 3.8630 100.00 1.5106 24 666.0 20.20 131.42 13.33 23.10 4.89822 0.00 18.100 0 0.6310 4.9700 100.00 1.3325 24 666.0 20.20 375.52 3.26 50.00 5.66998 0.00 18.100 1 0.6310 6.6830 96.80 1.3567 24 666.0 20.20 375.33 3.73 50.00 6.53876 0.00 18.100 1 0.6310 7.0160 97.50 1.2024 24 666.0 20.20 392.05 2.96 50.00 9.23230 0.00 18.100 0 0.6310 6.2160 100.00 1.1691 24 666.0 20.20 366.15 9.53 50.00 8.26725 0.00 18.100 1 0.6680 5.8750 89.60 1.1296 24 666.0 20.20 347.88 8.88 50.00 11.10810 0.00 18.100 0 0.6680 4.9060 100.00 1.1742 24 666.0 20.20 396.90 34.77 13.80 18.49820 0.00 18.100 0 0.6680 4.1380 100.00 1.1370 24 666.0 20.20 396.90 37.97 13.80 19.60910 0.00 18.100 0 0.6710 7.3130 97.90 1.3163 24 666.0 20.20 396.90 13.44 15.00 15.28800 0.00 18.100 0 0.6710 6.6490 93.30 1.3449 24 666.0 20.20 363.02 23.24 13.90
使用内置的 readmatrix 读取, 会出现以下两个问题:
1. 每行行首可能会出现空格, readmatrix 会得到第一个数据为 NaN;
2. 数据与数据之间虽然都是空格, 但空格数量不统一, 有1个空格、2个空格和3个空格几种情况。
所以使用 readmatrix 得到的数据列数不匹配,多分隔出来的数据全部都是 NaN.
对于上述两个问题,MATLAB 中的 readmatrix 函数是可以输入 "ConsecutiveDelimitersRule", "join" 把重复的分隔符合并成一个分隔符, "LeadingDelimitersRule", "ignore" 参数忽略行首的分隔符.
contains(str, pat) 函数用于判断字符串 str 中是否包含 pat 子串,但在 Windows 4.2.1 版本中,contains 像是被一个用于几何包含的函数给覆盖了


经过测试,该函数在 Linux 4.2.1 版本和 Windows 4.2.0 版本中都能正常运行。
Lévy 飞行是基于 Lévy 分布的随机搜索过程. Lévy 飞行是一种随机行走, 其中步长服从 Lévy 分布. 它通过模拟自然界中动物在寻找食物或迁徙过程中, 采取的长距离跳跃和短距离滑行相结合的移动模式. 其核心特点是步长的概率分布为重尾分布, 即存在相对较高的概率出现大跨步, 这使得动物能够在广阔的范围内进行搜索.
与传统的随机游走策略相比, Lévy 飞行策略具有以下优势:
* 提高搜索效率: 通过长距离跳跃, Lévy 飞行策略能够快速扩大搜索范围, 提高搜索效率;
* 跳出局部最优解: Lévy 飞行策略在搜索过程中偶尔会出现大跨步, 有助于跳出局部最优解, 寻找全局最优解;
* 适应性强: Lévy 飞行策略适用于各种复杂环境, 能够有效应对路径规划中的不确定性.
因此, Lévy 飞行算法作为一种高效的优化路径规划方法, 目前被广泛应用于智能优化算法中, 如麻雀搜索算法、鲸鱼优化算法、粒子群优化算法、蜣螂优化算法等等.
Mantegna 算法是 Mantegna 于 1994 年提出的用于模拟对称 Lévy 稳定过程. 根据 Mantegna 算法, 可以通过生成两个正态分布的数据计算得到服从 Lévy 分布的数据. 采用北太天元数值计算通用软件来实现该算法的代码如下:
function [s] = levyrnd(beta, m, n) %LEVYRND - Mantegna 算法生成对称 Lévy 稳定分布随机数组. % % 用法: % levyrng(beta); - 生成单个服从参数为 beta 的 Lévy 分布数据; % levyrng(beta, m); - 生成 m x m 维服从参数为 beta 的 Lévy 分布矩阵; % levyrng(beta, m, n); - 生成 m x n 维服从参数为 beta 的 Lévy 分布矩阵. % % 示例: % >> rng(1234); % >> levyrnd(1.8) % 0.5299 % >> levyrnd(0.5, 2) % 0.7074 -0.0853 % -2.1705 -219.2879 % >> levyrnd(1.1, 2, 3) % -0.6688 0.2140 -1.8900 % -3.4959 0.2340 -24.1111 % narginchk(1, 3); if nargin == 1 m = 1; n = 1; elseif nargin == 2 n = m; end % 计算 u ~ N(0, sigma^2) 的方差 num = gamma(1 + beta) * sin(pi * beta / 2); den = gamma((1 + beta)/2) * beta * 2^((beta - 1)/2); sigma = (num / den)^(1/beta); % 生成随机变量 u 和 v, v ~ N(0, 1). u = normrnd(0, sigma, m, n); v = normrnd(0, 1, m, n); % 生成 Lévy 分布数据 s = u ./ abs(v).^(1/beta); end
利用 Mantegna 算法, 可以生成一系列的服从 Lévy 分布的随机步长, 模拟 Lévy 飞行. 值得注意的是, 随机游走是在任意维度空间中, 一个点随机地向任意方向前进任意长度的距离, 然后不断的重复.
我们模拟从原点出发, 随机向任意方向前进步长为 $s$ 的 Lévy 飞行. 模拟过程如下:
clear;
clc;
% Lévy 分布参数
beta = 1.5;
% Lévy 飞行步数
n = 1000;
% 生成随机方向
angles = 2 * pi * rand(n, 1);
% 初始化数据
x = zeros(n + 1, 1);
y = zeros(n + 1, 1);
% 生成 Lévy 步长
s = levyrnd(beta, n, 1);
% 循环游走
for i = 1:n
x(i + 1) = x(i) + cos(angles(i)) * s(i);
y(i + 1) = y(i) + sin(angles(i)) * s(i);
end
% 绘制 Lévy 飞行随机游走
plot(x, y);
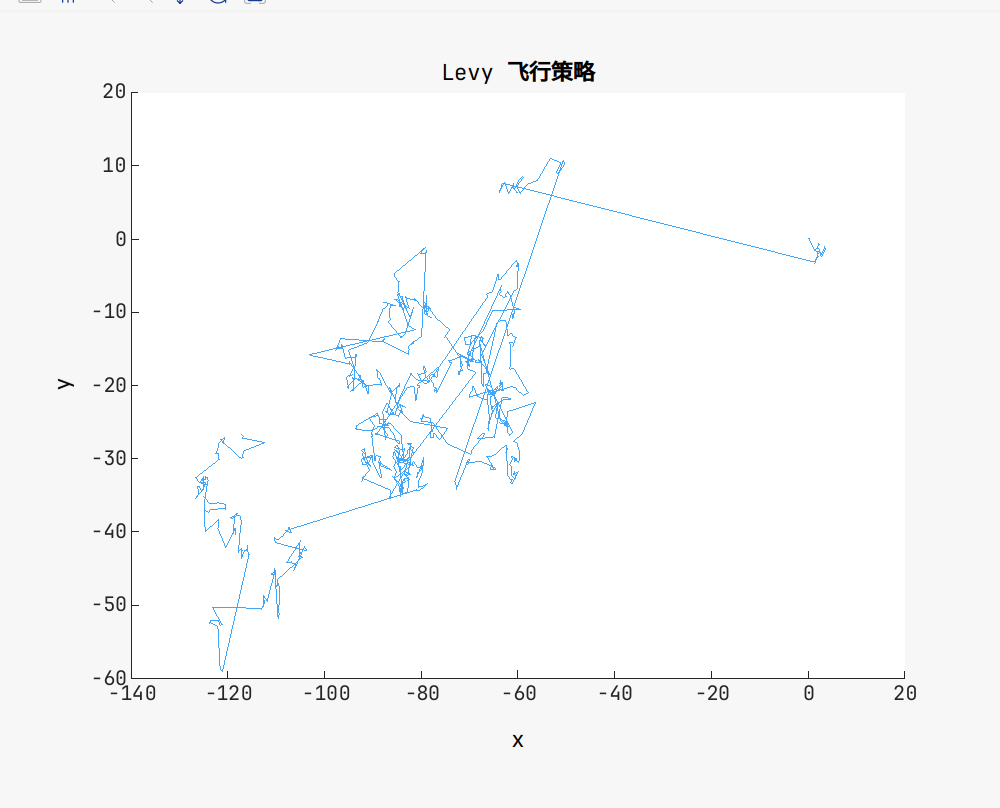
title("Levy 飞行策略");
xlabel("x");
ylabel("y");得到的结果如图所示:
对于 MATLAB 保存的 MAT 格式数据文件,在北太天元中只能读取 v6 和 v7 两个版本的数据文件,对于 v4 和 v7.3 两个版本的数据文件,在北太天元中均提示数据文件为空。
1. 对于可选位置参数 (addOptional) 和可选参数 (addParameter) 共同存在的情形, 仍不能正确的解析, 示例在原来的例子中加入 addRequired 如下:
function findArea(varargin)
p = inputParser;
p = addRequired(p, 'width', @(x) isnummeric(x) && isscalar(x) && (x > 0));
p = addOptional(p, 'height', 1);
p = addParameter(p, 'units', 'm');
p = addParameter(p, 'shape', 'square');
p = parse(p, varargin{:});
width = p.Results.width
height = p.Results.height
units = p.Results.units
shape = p.Results.shape
endfindArea(2, 3, "units", "cm") 现在可以正确解析了. 但是如果可选位置参数输入不足时, 如 findArea(2, "units", "cm") 就不能正常解析了.
在 inputParser 类的代码第 152 行定义的当前参数位置指针 pos = 1, 有一个必须参数和一个可选位置参数, pos 经过两次加一得到 pos = 3, 此时解析参数的时候, 剩余可选参数为 varargin(3:end) = "cm", "units" 虽然没有像之前的版本被赋值给 "height", 但也被吞掉消失. 只剩下 "units" 不是成对出现导致解析可选参数出错.
2. 在添加参数的时候, checkArgs(list, value, validator) 函数是通过 ismember 函数来判断是否存在该参数名的.
ismember 只能判断字符元胞数组, 那么在添加参数的时候只能使用字符数组, 如上面的示例 p = addOptional(p, 'width', 1); 原本使用的字符串在使用的时候就全部报错.
这个问题只需要在 inputParser 中添加几个 char 全部转化成字符数组即可, 而不用关心用户输入的是字符还是字符串.
分别是 addParameter 函数 101, 102 行 paramName 外面添加 char(), addOptional 函数 112, 113 行 paramName 外面添加 char(), addRequired 函数 123 行添加 char().
copyfile(source, destination) 用于复制文件. 在使用过程中存在以下几个问题
1. 如果 destination 不存在, 提示错误使用 copyfile 函数, 文件 destination 不存在, 这是 Windows 和 Linux 均存在的问题.
2. 创建一个空文件 destination, 此时再调用 copyfile 复制文件, Windows 平台可以成功复制, Linux 平台报错
cp: /opt/Baltamatica/lib/libattr.so.1: version `ATTR_1.3' not found (required by cp)
cp: /opt/Baltamatica/lib/libselinux.so.1: no version information available (required by cp)
cp: /opt/Baltamatica/lib/libselinux.so.1: no version information available (required by cp)
目前尝试的解决方案, 将系统的 libattr.so.1 和 libselinux.so.1 文件链接到 /opt/Baltamatica/lib 中
sudo mv /opt/Baltamatica/lib/libattr.so.1 /opt/Baltamatica/lib/libattr.so.1.bak
sudo mv /opt/Baltamatica/lib/libselinux.so.1 /opt/Baltamatica/lib/libselinux.so.1.bak
sudo ln -s /usr/lib/x86_64-linux-gnu/libattr.so.1 /opt/Baltamatica/lib/libattr.so.1
sudo ln -s /usr/lib/x86_64-linux-gnu/libselinux.so.1 /opt/Baltamatica/lib/libselinux.so.1
重新运行北太天元后可以复制已存在的文件.
1. Python 中的复数如何和北太天元中的复数相互转化. 这一点在 MATLAB 中也是没有相应的函数将 Python 的复数转化为 MATLAB 函数的复数, MATLAB 的机制是只要对 Python 的复数做了运算, 就自动转化为 MATLAB 的复数, 如 py.complex(1, 1) + 0 得到的就是 MATLAB 中的复数 1.0 + 1.0i.
2. 创建复数符号变量, sym(1+i) 不可行, 可行的两种方式, 直接使用符号虚数单位 sp.I 如 1 + sp.I, 另一种使用简化函数 sp.simplify() 或者封装好的 symsimplify(), 如 symsimplify(1+i);
3. SymPy 插件创建的符号变量不支持绝对值函数 abs(sym('x')).
4. SymPy 插件在调用 lambdify 函数时报错, 'NoneType' object has no attribute 'f_locals'. 示例如下:
load_plugin SymPy
sp = sympy_sp;
x = sym('x');
y = sin(x);
f = sp.lambdify(x, y)help format 得到的帮助文档对于有理数格式描述如下:分子或分母较大时用 * 符号代替。也可以简写为 RAT。
那么计算得到的 * 符号应该如何判断是分子较大还是分母较大呢? 重新换成 long 格式进行判断吗?
测试了一下,只有 1e-6 和 1e6 之间的数可以用有理数显示。
两年半前提出来的 在 WSL2 中使用北太天元 现在可以使用了:
现在在 WSL2 安装 Ubuntu24.04 发行版,尝试安装最新版的北太天元(中间其他版本的北太天元没有尝试过,也许有 2.1.3 到 4.2.1 之间的版本已经可以在 WSL2 中运行)
确保已经安装了 libnss3 和 gstreamer1.0-libav 软件包,如果没有安装,使用 apt install libnss3 gstreamer1.0-libav 进行安装
在终端下启动北太天元
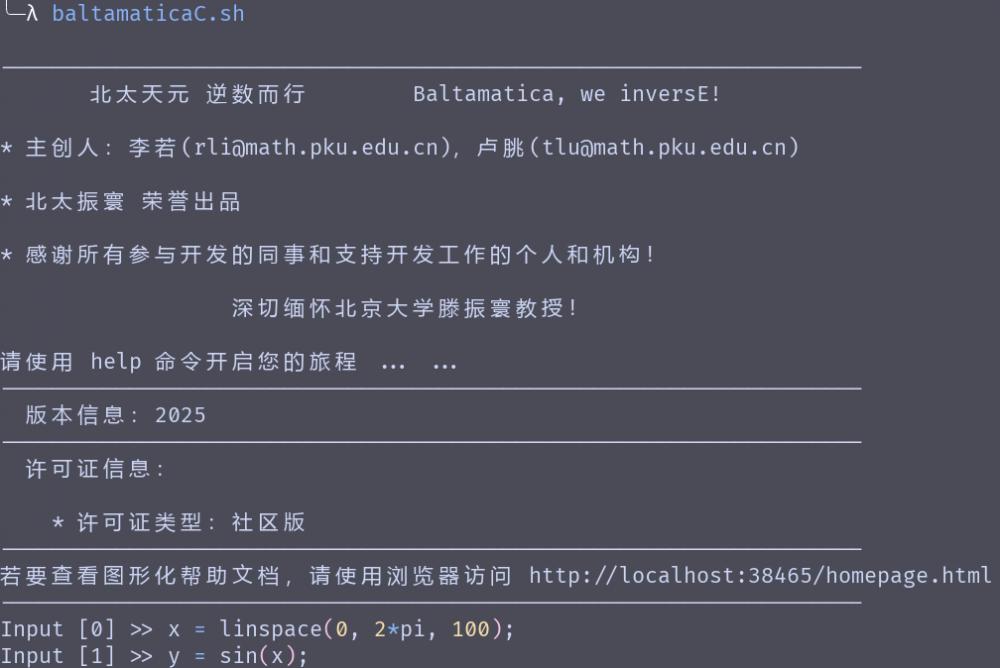
可以正常运行。但是最新版的北太天元删除了终端下使用绘图的功能,算是对去年提出来的问题 终端下无法启动绘图 的一种解决吧(不过好像没有删干净,gplot 依赖于 plot 但没有被删掉)
想要启动桌面版的北太天元,还需要确保安装 xcb-cursor 相关的依赖库:
apt install -y libxcb-cursor0 libxcb-xinerama0 libxcb-icccm4 libxcb-image0 libxcb-keysyms1 libxcb-randr0 libxcb-render-util0 libxcb-shape0 libxcb-sync1 libxcb-xfixes0 libxcb-xkb1
安装成功后,运行 baltamatica.sh 打开北太天元界面:

运行也没有问题。另外的一点感觉,2025 版的软件要比之前版本启动、关闭上都要慢上很多,另外在 WSL2 上使用似乎比 Windows 上使用反应要快。