以下内容为卢朓老师在B站进行的分享,可以作为学习参考:
GARCH族模型,即广义自回归条件异方差模型(Generalized Autoregressive Conditional Heteroskedasticity Model),是一类用于估计时间序列数据波动率的统计模型。该模型由Bollerslev在1986年提出,是对ARCH(自回归条件异方差)模型的一种重要扩展。GARCH模型在金融时间序列分析中具有广泛的应用价值,尤其是在金融市场波动性的建模和预测方面。
一、GARCH模型的基本概念
GARCH模型主要用于描述时间序列数据(如股票价格、汇率、利率等)的波动性特征。传统计量经济学假设时间序列变量的波动幅度(方差)是固定的,但这往往不符合实际情况。例如,股票收益的波动幅度通常会随时间变化,表现出聚集性特征,即大的波动后面往往跟着大的波动,小的波动后面往往跟着小的波动。GARCH模型通过引入条件异方差来描述这种波动性聚集现象,从而更准确地捕捉时间序列数据的波动性特征。
二、GARCH模型的结构
GARCH模型通常由两部分组成:均值方程和方差方程。
均值方程:通常是一个ARMA(自回归移动平均)模型,用于描述时间序列数据的线性关系。它表示时间序列数据在某一时刻的期望值,即数据的均值部分。
方差方程:是GARCH模型的核心,用于描述时间序列数据的波动性。方差方程是一个自回归移动平均模型,但作用于时间序列的方差上,而不是直接作用于时间序列数据本身。通过考虑过去的波动率和误差项,方差方程能够预测未来的波动率。
三、GARCH模型的数学表达式
GARCH模型的均值方程通常用于描述时间序列数据的条件均值,即数据在给定信息集下的期望值。然而,值得注意的是,GARCH模型的核心在于其方差方程,该方程用于刻画时间序列数据的条件异方差性,即波动性。尽管如此,在构建GARCH模型时,通常也会同时指定一个均值方程。
对于GARCH模型的均值方程,其形式可以相对简单,也可以相对复杂,具体取决于数据的特性和研究目的。一个常见的均值方程认为时间序列数据的均值是恒定的。这种方程形式适用于数据围绕某个固定水平波动的情况。
![]()
其中,y_t 是t时刻的观测值, \mu 是常数均值,\epsilon_t 是残差项。
在GARCH模型中,残差项 $\epsilon_t$ 通常被表示为条件方差 $\sigma_t$ 和一个独立同分布(iid)的随机变量 $z_t$ 的乘积,即
![]()
这里,$z_t$ 通常被假设为标准正态分布 $N(0,1)$ 的随机变量,意味着它有一个均值为0和方差为1的正态分布。
条件方差 $\sigma_t$ 是通过GARCH模型的方差方程来估计的,一般形式的GARCH(p,q)模型的方差方程可以表示为:
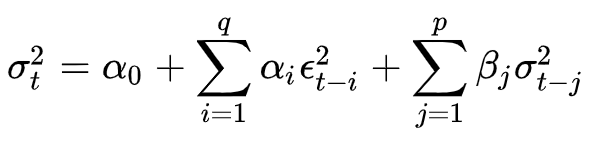
其中, 是t时刻的条件方差,ϵ_t 是t时刻的残差项,α_0 是常数项,α_i 和 β_j 是模型的参数。p和q分别表示方差方程中自回归项和移动平均项的阶数。
四、GARCH族模型的求解
GARCH族模型作为一类用于精确估计金融时间序列数据波动率的统计模型,其求解过程涉及多个复杂步骤。
首先,准备和预处理金融时间序列的历史数据是至关重要的。这一步骤包括数据的清洗、转换和差分等,以确保数据的准确性、一致性和适用性。通过预处理,我们可以消除数据中的异常值、填补缺失值,并将其转换为适合模型分析的形式。
接下来,根据数据的特性和研究需求,我们需要选择合适的GARCH模型,并明确设定均值方程和方差方程的形式。这一步骤要求我们具备扎实的统计理论知识,以便能够准确地描述时间序列数据的动态特征。
在模型设定之后,构建似然函数成为关键。似然函数是基于残差项的分布(如标准正态分布)来构建的,它反映了模型参数与观测数据之间的匹配程度。通过最大化似然函数,我们可以找到最优的参数估计值,从而使模型更好地拟合观测数据。
参数估计是求解GARCH族模型的核心步骤。我们需要运用极大似然估计法(MLE)等高级统计参数估计方法,并通过求解似然函数的导数等于零的方程组或使用迭代算法(如Newton-Raphson算法、BFGS算法等)来找到最优的参数估计值。这一步骤要求我们具备深厚的数学功底和编程能力,以便能够准确地估计出模型的参数。
最后,对估计得到的模型进行严格的检验是必不可少的。我们需要运用残差检验、模型验证等统计方法,评估模型的拟合效果和预测能力。如果模型通过检验,我们就可以使用它来进行时间序列数据的波动率预测和进一步的分析。
五、GARCH族模型的衍生与发展
随着研究的深入,GARCH模型得到了不断的扩展和完善,形成了GARCH族模型。这些衍生模型包括但不限于:
EGARCH:指数GARCH模型,用于解决GARCH模型中对正负扰动的对称性问题。
GJR-GARCH:Glosten-Jagannathan-Runkle GARCH模型,同样用于捕捉正负扰动对波动率的不对称影响。
APARCH:平均绝对偏差GARCH模型,通过引入绝对值项来改进模型。
IGARCH:积分GARCH模型,用于处理条件方差无限持久的情况。
GARCH-M:均值GARCH模型,在均值方程中引入方差项,以反映风险与收益之间的关系。
六、GARCH模型的应用
GARCH模型在金融市场中具有广泛的应用,主要包括:
波动性预测:通过对历史数据的分析,GARCH模型可以预测未来时间序列数据的波动性,为投资者提供决策支持。
风险管理:金融机构可以利用GARCH模型进行风险定价和风险管理,提高经营效率。
投资组合优化:投资者可以根据GARCH模型的预测结果调整投资组合,以降低投资风险并提高收益。
综上所述,GARCH族模型是一类强大的时间序列分析工具,特别适用于金融市场的波动性建模和预测。通过不断的研究和发展,GARCH模型在金融领域的应用前景将更加广阔。
七、北太天元的代码示例
% 示例数据(通常这里应该是金融时间序列数据,如股票收益率)
N = 1000; %数据点的总数
data = randn(N,1); % 使用随机数作为示例
% 设定初始值
mu = mean(data); % 样本均值
sigma2 = zeros(N,1); %和data 一样为列向量
sigma2(1) = var(data); % 样本方差
residuals = data - mu; % 计算残差
% 迭代计算GARCH(1,1)模型的条件方差(这里我们先使用简单的样本方差作为初始值)
omega = 0.01;
alpha = 0.1;
beta = 0.85;
for t = 2:length(data)
sigma2(t) = omega + alpha * residuals(t-1)^2 + beta * sigma2(t-1);
end
% 使用极大似然估计法(MLE)来估计参数
params0 = [omega, alpha, beta]; % 初始参数
options = optimset('Display','iter','TolFun',1e-8);
params_est = fminsearch(@(params) -logLikelihoodGARCH(params, residuals, sigma2), params0, options);
% 输出估计的参数
omega_est = params_est(1);
alpha_est = params_est(2);
beta_est = params_est(3);
fprintf('Estimated omega: %f\n', omega_est);
fprintf('Estimated alpha: %f\n', alpha_est);
fprintf('Estimated beta: %f\n', beta_est);
% 辅助函数:计算GARCH(1,1)模型的对数似然函数
function ll = logLikelihoodGARCH(params, residuals, sigma2)
omega = params(1);
alpha = params(2);
beta = params(3);
% 这里我们不重新计算残差和条件方差,而是使用传入的参数
% 计算对数似然函数
T = length(residuals);
ll = -0.5 * sum(log(2*pi*sigma2(2:T)) + residuals(2:T).^2 ./ sigma2(2:T));
% 注意:我们从第二个观测值开始计算对数似然,因为第一个观测值的条件方差是已知的(通常是样本方差)
end代码可以copy 到文心一言里,让它给你解读一下, 这里仅仅解释一下对数似然函数。对数似然函数是根据GARCH(1,1)模型的定义和假设来推导的。GARCH(1,1)模型是一个时间序列模型,用于描述金融资产的波动率。它假设时间序列的残差(去均值化后的观测值)服从一个条件正态分布,其条件方差由过去的残差和过去的条件方差共同决定。
具体来说,GARCH(1,1)模型可以表示为:
![]()
其中,$\sigma_t^2$ 是时刻t的条件方差,$\omega$、$\alpha$ 和 $\beta$ 是模型的参数,$r_{t-1}$ 是时刻t-1的残差。
现在,我们假设残差 $r_t$ 服从条件正态分布 $N(0, \sigma_t^2)$。这意味着,给定过去的信息,$r_t$ 的概率密度函数是:
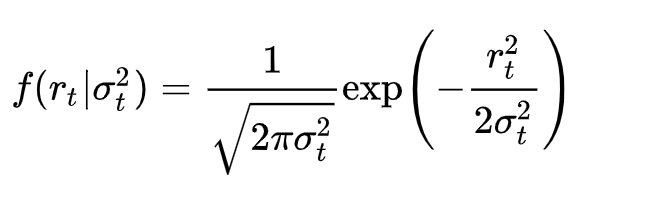
对数似然函数是概率密度函数的自然对数,即:
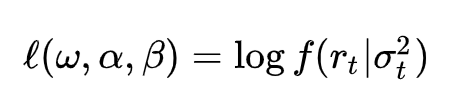
由于我们处理的是一系列观测值 $r_2, \ldots, r_T$(通常第一个观测值用于初始化),对数似然函数是这些观测值的对数概率密度之和:
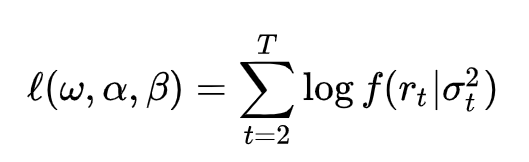
将概率密度函数代入上式,并取对数,我们得到:
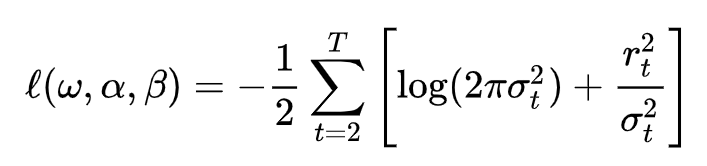
这就是我们在代码中使用的对数似然函数的形式。注意,这里有一个负号,因为我们在最大化对数似然函数时实际上是在最小化负对数似然函数(这是一个常见的做法,因为优化算法通常设计为最小化目标函数)。因此,当我们使用`fminsearch`函数时,我们实际上是在最小化负对数似然函数,这等价于最大化对数似然函数。

七、北太天元V3.5的一个小bug的修复
北太天元报错:
错误(文件 C:\baltamatica\plugins\optimization\scripts\fminsearch.m, 行474, 列1): 与function配对的end一旦出现一个以上,就必须做到一一对应。现在是没有做到一一对应。
C:\baltamatica\plugins\optimization\scripts\fminsearch.m解析出错
修复方法:
在 C:\baltamatica\plugins\optimization\scripts\fminsearch.m的471行后面增加一行,内容是end
增加后, 如下图所示

相关视频讲解:
