1、聚类(Clustering):
聚类是一个将数据集划分为若干(class)或类(cluster)的过程,并使得同一个组内的数据对象具有较高的相似度;而不同组中的数据对象是不相似的。
相似或不相似是基于数据描述属性的取值来确定的,通常利用各数据对象间的距离来进行表示。聚类分析尤其适合用来探讨样本间的相互关联关系从而对一个样本结构做一个初步的评价。
2、聚类与分类的区别
聚类是一种无(教师)监督的学习方法。与分类不同,其不依赖于事先确定的数据类别,以及标有数据类别的学习训练样本集合。 因此,聚类是观察式学习,而不是示例式学习。
3、什么是好的聚类
一个好的聚类方法将产生以下的高聚类:
最大化类内的相似性
最小化类间的相似性
聚类结果的质量依靠所使用度量的相似性和它的执行。聚类方法的质量也可以用它发现一些或所有隐含模式的能力来度量。
聚类分析有两种:
一种是对样品的分类,称为Q型,
一种是对变量(指标)的分类,称为R型。
R型聚类分析的主要作用:
(1) 不但可以了解个别变量之间的亲疏程度,而且可以了解各个变量组合之间的亲疏程度。
(2) 根据变量的分类结果以及它们之间的关系,可以选择主要变量进行Q型聚类分析或回归分析。(R2为选择标准)
Q型聚类分析的主要作用:
(1) 可以综合利用多个变量的信息对样本进行分析
(2) 分类结果直观,聚类谱系图清楚地表现数值分类结果
(3) 聚类分析所得到的结果比传统分类方法更细致、全面、合理。
1、常用距离的定义


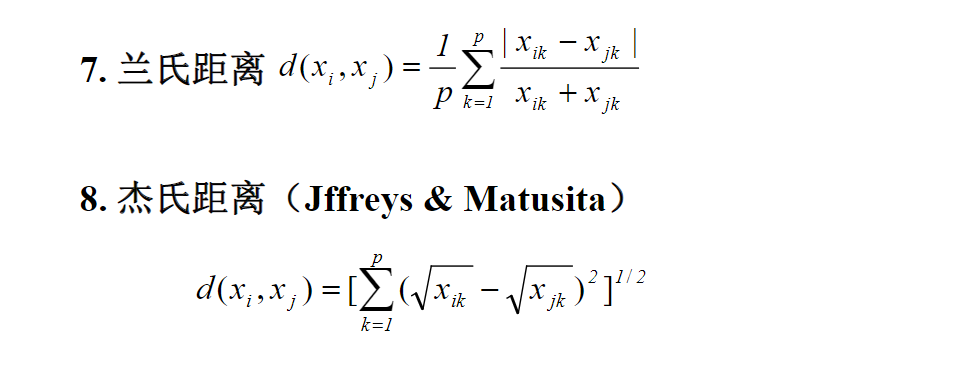
2、相似系数



3、类间距离

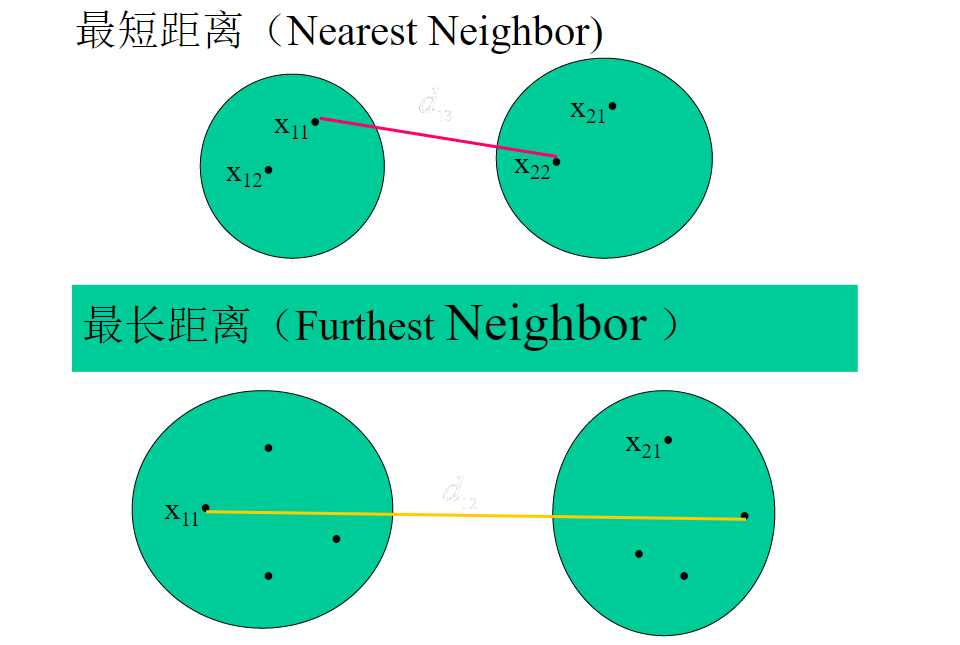

1、谱系聚类算法的步骤:
(1)选择样本间距离的定义及类间距离的定义
(2)计算n个样本之间的距离,得到距离矩阵
(3)构造个类,每类只含有一个样本
(4)合并符合类间距离要求的两类为一个新类
(5)计算新类与当前各类的距离。若类的个数为1,则转到步骤6,否则回到步骤4
(6)画出聚类图
(7)决定类的个数和类


1、K-平均聚类算法步骤:
(1)从n个数据对象任意选择k个对象作为初始聚类中心
(2)循环 (3)到 (4)直到每个聚类不再发生变化为止
(3)根据每个聚类对象的均值(中心对象 ),计算每个对象与这些中心对象的距离,并根据最小距离重新对相应对象进行划分:
(4)重新计算每个(有变化)聚类的均值(中心对象)
2、算法的基本思想:
(1)首先,随机的选择k个对象,每个对象初始的代表了一个簇的平均值;
(2)对剩余的每个对象,根据其与各个簇中心的距离,将它赋给最近的簇;
(3)然后重新计算每个簇的平均值。
(4)这个过程不断重复,直到准则函数收敛。
3、算法的特点:
只适用于聚类均值有意义的场合,在某些应用中,如:数据集中包含符号属性时,直接应用k-means算法就有问题。
用户必须事先指定k的个数。对噪声和孤立点数据敏感,少量的该类数据能够对聚类均值起到很大的影响。
本文转自公众号“数学建模老哥”
